Difference between revisions of "Triggers:GRBs"
Jure.Japelj (talk | contribs) |
Jure.Japelj (talk | contribs) |
||
| Line 29: | Line 29: | ||
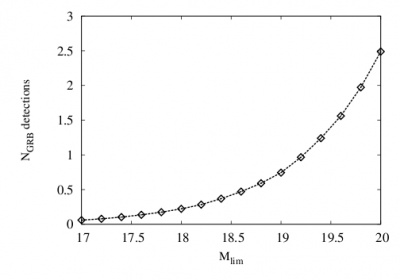
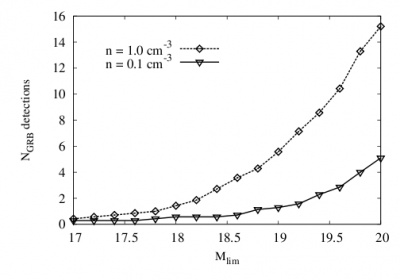
Number of detections in respect to limiting magnitude are shown on the the right in the top and bottom figure for the case of on-axis and orphan afterglows, respectively. The average GRB orphan-afterglow detection rate has been simulated for two different circumburst environments. | Number of detections in respect to limiting magnitude are shown on the the right in the top and bottom figure for the case of on-axis and orphan afterglows, respectively. The average GRB orphan-afterglow detection rate has been simulated for two different circumburst environments. | ||
| − | |||
| − | |||
[[File:F3.jpg|400px|left]] | [[File:F3.jpg|400px|left]] | ||
[[File:F4.jpg|400px|left]] | [[File:F4.jpg|400px|left]] | ||
| + | |||
| + | Figure 6 shows initial magnitude distribution of detected on-axis afterglows (black), same distribution at the time of the first detection (gray) and the distribution of detections with the second telescope. Similar plot for orphan afterglows is given in $\cite{japelj2}$. | ||
Since GRB afterglows are initially rapidly fading and they will be observed for 4.4 seconds by each CCD camera, the change of magnitude in that time could in principle be observable. For all detected afterglows in our simulations, we therefore calculated the change of magnitude in 4.4 s, corresponding to observations by two successive CCDs, and also for observations lasting as long as a specific afterglow is in the telescope's field of view. The distribution of the change of magnitude for both cases is shown in Figure 7. Since the expected photometric error of Gaia at $M_{\rm lim} = 20$ mag will be 10 mmag at best (but probably bigger [http://www.rssd.esa.int/index.php?project=GAIA&page=index ESA]), the chances of observing the change in magnitudes will be small. | Since GRB afterglows are initially rapidly fading and they will be observed for 4.4 seconds by each CCD camera, the change of magnitude in that time could in principle be observable. For all detected afterglows in our simulations, we therefore calculated the change of magnitude in 4.4 s, corresponding to observations by two successive CCDs, and also for observations lasting as long as a specific afterglow is in the telescope's field of view. The distribution of the change of magnitude for both cases is shown in Figure 7. Since the expected photometric error of Gaia at $M_{\rm lim} = 20$ mag will be 10 mmag at best (but probably bigger [http://www.rssd.esa.int/index.php?project=GAIA&page=index ESA]), the chances of observing the change in magnitudes will be small. | ||
To summarise: the number of expected orphan afterglow detections with the Gaia satellite during it's five years of expected operation is of the order of 10. Adding the results of the on-axis afterglows simulation, the number of expected optical afterglow detections in five years is slightly increased. The problem of afterglow recognition and poor time sampling of the lightcurve, in addition to the small number of expected detections, makes the study of GRB optical afterglows with Gaia difficult. On the other hand, since orphan afterglows have not been conclusively detected yet, a possible detection would provide valuable new data. | To summarise: the number of expected orphan afterglow detections with the Gaia satellite during it's five years of expected operation is of the order of 10. Adding the results of the on-axis afterglows simulation, the number of expected optical afterglow detections in five years is slightly increased. The problem of afterglow recognition and poor time sampling of the lightcurve, in addition to the small number of expected detections, makes the study of GRB optical afterglows with Gaia difficult. On the other hand, since orphan afterglows have not been conclusively detected yet, a possible detection would provide valuable new data. | ||
Revision as of 15:12, 31 March 2011
Gamma-Ray Burst Optical Afterglows
Gamma-ray bursts (GRBs) are extremely energetic, brief and unpredictable explosions occuring on cosmological distances. They represent the most luminous events in the gamma-ray part of the electromagnetic spectrum known in the universe. Often, the prompt gamma-ray emission is followed by an afterglow emitted at longer wavelengths (from X-rays to radio), which can last for several days. Comprehensive review on GRBs and their physics can be found in Piran 2004 or Meszaros 2006.
GRB explosions are believed to be collimated, rather than spherical Granot 2007. Thus the material, ejected by the explosion, is expanding in the form of a bimodal jet, characterized by an initial half-opening angle \theta_{j}. The shape of the lightcurve depends on the relative position of the observer's line-of-sight and the axis of the jet cone. We can describe that with an angle $\theta_{\rm obs}$ between both directions. We talk about an on-axis GRB and a 'regular' optical afterglow when $\theta_{\rm obs} < \theta_{\rm j}$. In the case of $\theta_{\rm obs} > \theta_{\rm j}$, we can not observe the prompt gamma-ray emission. Due to the beaming effect, we could still observe the so called orphan afterglow (details in Granot 2007 or ). A schematic afterglow lightcurves for different jet half-opening angles and viewing angles are shown in figure on the right.
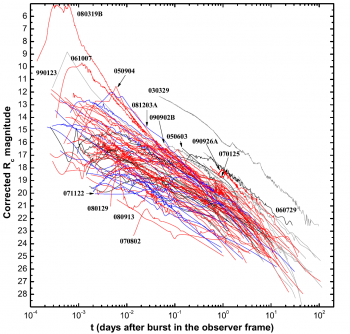
A large sample of observed optical lightcurves of regular 'on-axis' afterglows is shown in figure on the left (Kann et al. 2010).
Observations made by the Swift satellite imply that there are approximately 300 on-axis GRBs per year for which we could observe an optical afterglow.
Even though orphan afterglows have not been conclusively detected yet, they have been studied a great deal over the last 15 years and various estimations on their detectability have been made (Granot 2007 and references therein).
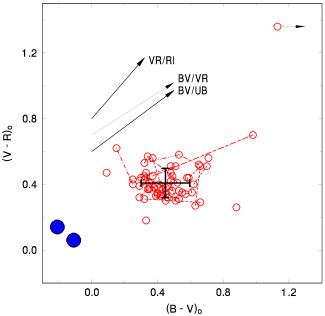
It has been observed, that the color indices (R - I), (V -R) and (B - V) of a sample of observed afterglows are roughly constant in the first 10 days of observation, i.e. their time evolution is negligible. This property could serve as a mean to recognize an afterglow and to distinguish it from other possible sources Šimon et al. 2001 Šimon et al. 2004. Color-color (B-V vs. V-R) diagram of optical afterglows of long GRBs is shown in figure on the right. All the color indices were corrected for the Galactic reddening. Multiple indices of the same optical afterglow are connected by lines for convenience. Optical afterglows of the ensemble are denoted by open red circles. The mean colors (centroid) of the whole ensemble, including the standard deviations, are marked by the large cross. The outlying optical afterglow of GRB 060218 (closed blue circles) is not included in the calculation of the centroid. The representative reddening paths for E(B-V) = 0.5 mag are shown; they show how much and where the observed data point would move without proper correction (even erroneous correction would thus shift the point only slightly and in predictable direction). Adapted from Šimon et al. 2001 Šimon et al. 2004 where a detailed information can be found.
Detecting GRBs with Gaia
In order to predict the number of optical afterglow detections with Gaia in five years of it's time of operation, a simulation was performed. The simulation took into account a scanning law of Gaia, it's field of view, etc. It consists of two parts: one for regular 'on-axis' afterglows and the other for orphan afterglows. In the former the observational data were used to constrain the parameters needed in the simulation (i.e. initial afterglow magnitude distribution, number of afterglows occuring in five years, etc.), while in the latter the parameters were obtained from theoretical predictions. Details of on-axis and orphan afterglow simulation are given in $\cite{japelj}$ and $\cite{japelj2}$, respectively.
Number of detections in respect to limiting magnitude are shown on the the right in the top and bottom figure for the case of on-axis and orphan afterglows, respectively. The average GRB orphan-afterglow detection rate has been simulated for two different circumburst environments.
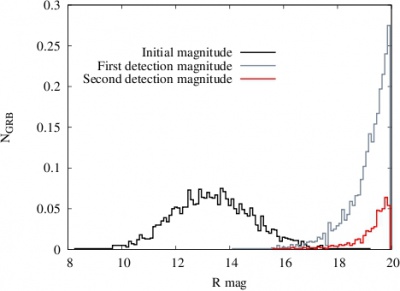
Figure 6 shows initial magnitude distribution of detected on-axis afterglows (black), same distribution at the time of the first detection (gray) and the distribution of detections with the second telescope. Similar plot for orphan afterglows is given in $\cite{japelj2}$.
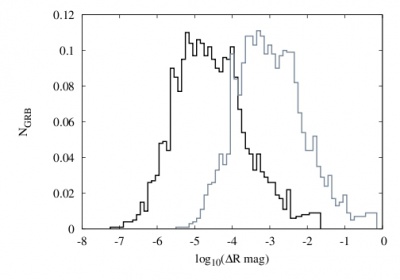
Since GRB afterglows are initially rapidly fading and they will be observed for 4.4 seconds by each CCD camera, the change of magnitude in that time could in principle be observable. For all detected afterglows in our simulations, we therefore calculated the change of magnitude in 4.4 s, corresponding to observations by two successive CCDs, and also for observations lasting as long as a specific afterglow is in the telescope's field of view. The distribution of the change of magnitude for both cases is shown in Figure 7. Since the expected photometric error of Gaia at $M_{\rm lim} = 20$ mag will be 10 mmag at best (but probably bigger ESA), the chances of observing the change in magnitudes will be small.
To summarise: the number of expected orphan afterglow detections with the Gaia satellite during it's five years of expected operation is of the order of 10. Adding the results of the on-axis afterglows simulation, the number of expected optical afterglow detections in five years is slightly increased. The problem of afterglow recognition and poor time sampling of the lightcurve, in addition to the small number of expected detections, makes the study of GRB optical afterglows with Gaia difficult. On the other hand, since orphan afterglows have not been conclusively detected yet, a possible detection would provide valuable new data.